Reproducing Polynomials with B-Splines: Unterschied zwischen den Versionen
Niki (Diskussion | Beiträge) |
Niki (Diskussion | Beiträge) |
||
| (14 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | <section begin="head"/> | ||
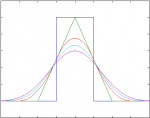
| + | [[Datei:bspline_family.png|right|150px|Family of B-splines up to N=4]] | ||
A B-Spline of order <math>N</math> is known to be able to reproduce any polynomial up to order <math>N</math>: | A B-Spline of order <math>N</math> is known to be able to reproduce any polynomial up to order <math>N</math>: | ||
| Zeile 8: | Zeile 10: | ||
An important question is how to obtain the coefficients <math>c_{m,n}</math> for the reproduction-formula. In this small article, I describe one way. | An important question is how to obtain the coefficients <math>c_{m,n}</math> for the reproduction-formula. In this small article, I describe one way. | ||
| + | <section end="head"/> | ||
| + | |||
| + | Starting from | ||
| + | |||
| + | <math> | ||
| + | \sum_{n \in \mathbb{Z}} c_{m,n} \varphi(t - n) = t^m | ||
| + | </math> | ||
| + | |||
| + | the coefficients can be obtained using the dual of <math>\varphi</math>, <math>\tilde{\varphi}</math><ref>P.L. Dragotti, M. Vetterli, T.Blu: "Sampling Moments and Reconstructing Signals of Finite Rate of Innovation: Shannon Meets Strang-Fix", ''IEEE Transactions on Signal Processing'', vol. 55, No. 5, May 2007</ref> (I set <math>\beta_N = \varphi</math> for consistency with my notes): | ||
| + | |||
| + | <math> | ||
| + | c_{m,n} = \int_{-\infty}^{\infty} t^m \tilde{\varphi}(t - n)\,dt | ||
| + | </math> | ||
| + | |||
| + | However, even if the dual would be known, solving the infinite integral is only feasible when the dual has finite support. This is the case with the B-Spline itself but not with its dual! | ||
| + | |||
| + | A closer look at the formula tells that this is nothing more than a convolution (under the assumption that <math>\tilde{\varphi}</math> is symmetric which is the case): | ||
| + | |||
| + | <math> | ||
| + | c_{m,n} = \int t^m \tilde{\varphi}(-(n-t))\,dt = \int t^m \tilde{\varphi}(n-t)\,dt = (t^m * \tilde{\varphi})(n) | ||
| + | </math> | ||
| + | |||
| + | Now, this can be transformed to fourier domain: | ||
| + | |||
| + | <math> | ||
| + | (t^m * \tilde{\varphi})(n) = \mathcal{F}^{-1}\left\{ \mathcal{F}\left\{t^m\right\} \tilde{\Phi}(\omega)\right\} = \mathcal{F}^{-1}\left\{ j^m \sqrt{2\pi} \delta^{(n)}(\omega) \tilde{\Phi}(\omega) \right\} = j^m \sqrt{2\pi} \mathcal{F}^{-1}\left\{\delta^{(n)}(\omega) \tilde{\Phi}(\omega) \right\} | ||
| + | </math> | ||
| + | |||
| + | Writing the inverse of this expression yields: | ||
| + | |||
| + | <math> | ||
| + | j^m \sqrt{2\pi} \frac{1}{\sqrt{2\pi}} \int_{-\pi}^{\pi} \delta^{(n)}(\omega) \tilde{\Phi}(\omega) e^{j\omega n}\,d\omega = j^m \int_{-\infty}^{\infty} \delta^{(n)}(\omega) \underbrace{\tilde{\Phi}(\omega) e^{j\omega n}}_{f(\omega)}\,d\omega | ||
| + | </math> | ||
| + | |||
| + | It is known that<ref>http://en.wikipedia.org/wiki/Dirac_delta_function</ref>: | ||
| + | |||
| + | <math> | ||
| + | \int \delta^{(n)}(x) f(x)\,dx = (-1)^n f^{(n)}(0) | ||
| + | </math> | ||
| + | |||
| + | so that | ||
| + | |||
| + | <math> | ||
| + | j^m \int_{-\infty}^{\infty} \delta^{(n)}(\omega) f(\omega)\,d\omega = j^m (-1)^m \left. \frac{\partial^m}{\partial \omega^m} f(\omega) \right|_{\omega = 0} | ||
| + | </math> | ||
| + | |||
| + | Now the whole procedure has been reduced to calculating the derivative of <math>f(\omega)</math> and set the result to zero. | ||
| + | |||
| + | An open question is how to obtain the dual of <math>\varphi</math>. As the reproduction formula spans a vector space, <math>\varphi</math> must be at least bi-orthogonal to <math>\tilde{\varphi}</math>. This translates in fourier domain to<ref>S. Mallat: "A Wavelet Tour of Signal Processing", ''Academic Press'' 1999</ref>: | ||
| + | |||
| + | <math> | ||
| + | \tilde{\Phi}(\omega) = \frac{\Phi(\omega)}{\sum_{k \in \mathbb{Z}} |\Phi(\omega + 2\pi k)|^2} | ||
| + | </math> | ||
| + | |||
| + | The fourier transform of a B-Spline of order <math>N</math> is (e.g. <ref>M.Unser: "Splines - A Perfect Fit for Signal and Imaging Processing", ''IEEE Signal Processing Magazine'' Nov. 1999</ref>): | ||
| + | |||
| + | <math> | ||
| + | \Beta_N(\omega) = \Phi(\omega) = \left( \frac{\sin(\omega/2)}{\omega/2} \right)^{N+1} = | ||
| + | \mathrm{sinc}^{N+1}(\omega/2) | ||
| + | </math> | ||
| + | |||
| + | The following derivation of the sum is borrowed from <ref>M.J.C.S. Reis, P.J.S.G. Ferreira, S.F.S.P. Soares: "Linear combinations of B-splines as generating functions for signal approximation", ''Elsevier Digital Signal Processing 15'', 2005</ref>. For this derivation to work, I set <math>L=N+1</math> temporarily: | ||
| + | |||
| + | <math> | ||
| + | \sum_{k \in \mathbb{Z}} |\Phi(\omega + 2\pi k)|^2 = | ||
| + | \sum_{k \in \mathbb{Z}} \left|\mathrm{sinc}\left(\frac{1}{2}(\omega + 2\pi k)\right)^L \right|^2 = | ||
| + | \sum_{k \in \mathbb{Z}} \left|\mathrm{sinc}\left(\frac{1}{2}(\omega + 2\pi k)\right) \right|^{2L} | ||
| + | </math> | ||
| + | |||
| + | and because <math>2L</math> is always even: | ||
| + | |||
| + | <math> | ||
| + | = \sum_{k \in \mathbb{Z}}\frac{\sin^{2L}(\frac{1}{2}(\omega + 2\pi k))}{\left(\frac{1}{2}(\omega + 2\pi k)\right)^{2L}} | ||
| + | = \sum_{k \in \mathbb{Z}}\frac{\sin^{2L}(\frac{\omega}{2} + \pi k))}{(\frac{\omega}{2} + \pi k)^{2L}} | ||
| + | </math> | ||
| + | |||
| + | Because of the periodicity it is known that | ||
| + | |||
| + | <math> | ||
| + | \sin^{2L}(x + \pi k) = \sin^{2L}(x) | ||
| + | </math> | ||
| + | |||
| + | such that | ||
| + | |||
| + | <math> | ||
| + | = \sin^{2L}\left(\frac{\omega}{2}\right) \sum_{k \in \mathbb{Z}}\frac{1}{(\frac{\omega}{2} + \pi k)^{2L}} | ||
| + | </math> | ||
| + | |||
| + | And finally the following relation is used<ref>L.V. Ahlfors: "Complex Analysis", ''McGraw-Hill'', 1979</ref>: | ||
| + | |||
| + | <math> | ||
| + | \sum_k \frac{1}{(x + \pi k)^{2L}} = -\frac{1}{(2L-1)!} \frac{d^{2L-1}}{dx^{2L-1}} \cot{x} | ||
| + | </math> | ||
| + | |||
| + | in order to finally obtain: | ||
| + | |||
| + | <math> | ||
| + | \sum_{k \in \mathbb{Z}} \left|\mathrm{sinc}\left(\frac{1}{2}(\omega + 2\pi k)\right)^L \right|^2 = | ||
| + | -\sin^{2L}\left(\frac{\omega}{2}\right) \frac{1}{(2L-1)!} \frac{d^{2L-1}}{d\left(\frac{\omega}{2}\right)^{2L-1}} \cot{\left(\frac{\omega}{2}\right)} | ||
| + | </math> | ||
| + | |||
| + | and with <math>L = N+1</math>: | ||
| + | |||
| + | <math> | ||
| + | \sum_{k \in \mathbb{Z}} |\Phi(\omega + 2\pi k)|^2 = | ||
| + | -\sin^{2(N+1)}\left(\frac{\omega}{2}\right) \frac{1}{(2N+1)!} \frac{d^{2N+1}}{d\left(\frac{\omega}{2}\right)^{2N+1}} \cot{\left(\frac{\omega}{2}\right)} | ||
| + | </math> | ||
| + | |||
| + | Therefore, together with <math>\Phi(\omega)</math> this yields: | ||
| + | |||
| + | <math> | ||
| + | \tilde{\Phi}(\omega) = \frac{(2N+1)!}{\left(\frac{\omega}{2}\right) \sin\left(\frac{\omega}{2}\right)^{N+1} \frac{d^{2N+1}}{d\left(\frac{\omega}{2}\right)^{2N+1}} \cot{\left(\frac{\omega}{2}\right)}} | ||
| + | </math> | ||
| + | |||
| + | and finally substituting for <math>t(\omega)</math>: | ||
| + | |||
| + | <math> | ||
| + | f(\omega) = \frac{(2N+1)!}{\left(\frac{\omega}{2}\right) \sin\left(\frac{\omega}{2}\right)^{N+1} \frac{d^{2N+1}}{d\left(\frac{\omega}{2}\right)^{2N+1}} \cot{\left(\frac{\omega}{2}\right)}} e^{j \omega n} | ||
| + | </math> | ||
| + | |||
| + | As this function is not well defined it is better to use the limit: | ||
| + | |||
| + | <math> | ||
| + | c_{m,n} = j^m \lim_{\omega \rightarrow 0} f(\omega) | ||
| + | </math> | ||
| + | |||
| + | = Examples for a cubic spline = | ||
| + | |||
| + | For a cubic spline (N=3) the coefficients are: | ||
| + | |||
| + | <math> | ||
| + | \begin{array}{lcl} | ||
| + | c_{0,n} & = & 1 \\ | ||
| + | c_{1,n} & = & n \\ | ||
| + | c_{2,n} & = & \frac{1}{3}\left( -1 + 3n^2 \right) \\ | ||
| + | c_{3,n} & = & -n + n^3 | ||
| + | \end{array} | ||
| + | </math> | ||
| + | |||
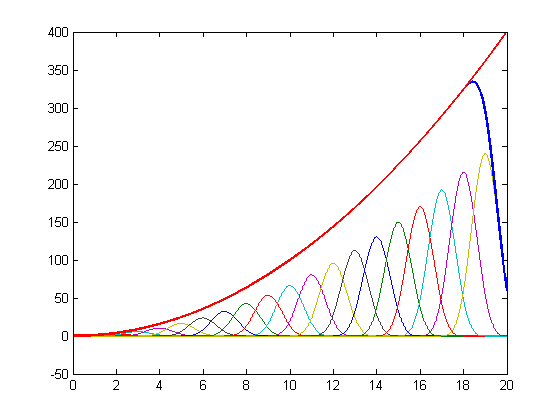
| + | [[Datei:poly_repro_quad.png|center|cubic spline reproducing polynomial of order 2]] | ||
| + | |||
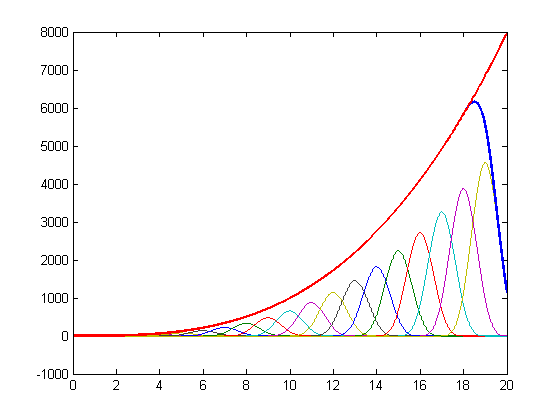
| + | [[Datei:poly_repro_cubic.png|center|cubic spline reproducing polynomial of order 3]] | ||
| + | |||
| + | = References = | ||
| + | |||
| + | <ref name="schoenberg">I.J. Schoenberg: "Cardinal interpolation and spline functions", ''J. Approx. Theory volume 2'', pp. 167-206, 1969</ref> | ||
| + | |||
| + | <references/> | ||
| + | |||
| + | = Comments = | ||
| + | |||
| + | <comments />{{:{{TALKSPACE}}:{{PAGENAME}}}} | ||
| + | |||
| + | [[Kategorie:Weblog]] | ||
Aktuelle Version vom 19. Juli 2010, 15:45 Uhr
A B-Spline of order is known to be able to reproduce any polynomial up to order :
In words, a proper linear combination of shifted versions of a B-Spline can reproduce any polynomial up to order . This is needed for different applications, for example, for the Sampling at Finite Rate of Innovation (FRI) framework. In this case any kernel reproducing polynomials (that is, satisfying the Strang-Fix conditions) can be used. However, among all possible kernels, the B-Splines have the smallest possible support.
An important question is how to obtain the coefficients for the reproduction-formula. In this small article, I describe one way.
Starting from
the coefficients can be obtained using the dual of , [1] (I set for consistency with my notes):
However, even if the dual would be known, solving the infinite integral is only feasible when the dual has finite support. This is the case with the B-Spline itself but not with its dual!
A closer look at the formula tells that this is nothing more than a convolution (under the assumption that is symmetric which is the case):
Now, this can be transformed to fourier domain:
Writing the inverse of this expression yields:
It is known that[2]:
so that
Now the whole procedure has been reduced to calculating the derivative of and set the result to zero.
An open question is how to obtain the dual of . As the reproduction formula spans a vector space, must be at least bi-orthogonal to . This translates in fourier domain to[3]:
The fourier transform of a B-Spline of order is (e.g. [4]):
The following derivation of the sum is borrowed from [5]. For this derivation to work, I set temporarily:
and because is always even:
Because of the periodicity it is known that
such that
And finally the following relation is used[6]:
in order to finally obtain:
and with :
Therefore, together with this yields:
and finally substituting for :
As this function is not well defined it is better to use the limit:
Examples for a cubic spline
For a cubic spline (N=3) the coefficients are:
References
- ↑ P.L. Dragotti, M. Vetterli, T.Blu: "Sampling Moments and Reconstructing Signals of Finite Rate of Innovation: Shannon Meets Strang-Fix", IEEE Transactions on Signal Processing, vol. 55, No. 5, May 2007
- ↑ http://en.wikipedia.org/wiki/Dirac_delta_function
- ↑ S. Mallat: "A Wavelet Tour of Signal Processing", Academic Press 1999
- ↑ M.Unser: "Splines - A Perfect Fit for Signal and Imaging Processing", IEEE Signal Processing Magazine Nov. 1999
- ↑ M.J.C.S. Reis, P.J.S.G. Ferreira, S.F.S.P. Soares: "Linear combinations of B-splines as generating functions for signal approximation", Elsevier Digital Signal Processing 15, 2005
- ↑ L.V. Ahlfors: "Complex Analysis", McGraw-Hill, 1979
- ↑ I.J. Schoenberg: "Cardinal interpolation and spline functions", J. Approx. Theory volume 2, pp. 167-206, 1969
Comments
<comments />































Bussi
--Manu 19:47, 19. Jul. 2010 (MSD)